Order of Operations Worksheets
PEMDAS Step by Step

These order of operations worksheets teach the way to figure equations in the correct order, step by step like shown in the Saxon Math books.

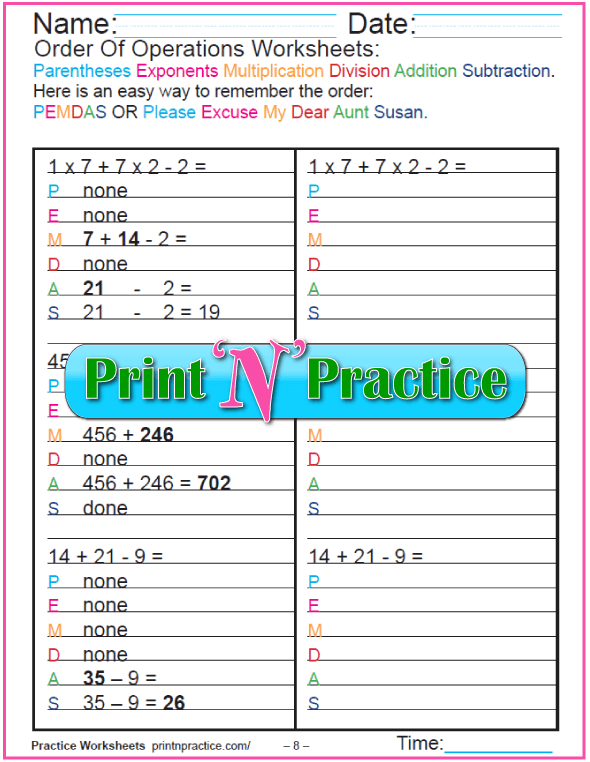
Remember that exponents come second in the order of operations for Pre-Algebra. This phrase makes it easy to remember that PEMDAS Stands For:

"Please excuse my dear Aunt Sara." or use the phrase PEMDAS for solving what is in the Parentheses first, the Exponents next, Multiplication and Division, and finally Addition and Subtraction - all from left to right. 

Use this phrase to remember the order when using the worksheets lower on this page.

Exponents come second in the order of operations for Pre-Algebra. Use this phrase to remember the order: "Please excuse my dear Aunt Sara." or use the phrase PEMDAS. 

PEMDAS Rule

Memorize the PEMDAS line.

Parenthesis, exponents, multiplication, division, addition, and subtraction; but remember that in the real world multiplication and division are of equal priority as are addition and subtraction. These order of operations worksheets teach it this way because the math books do and it's easy to remember.

The phrase "Please excuse my dear Aunt Sara." is cute and short. It works well with guided problem solving and you must use that formula if your Math textbooks use it, because you'll get a wrong answer if you don't. Memorization makes Math easier, so memorize that operations of equal priority should be worked left to right - usually. See what we found at Wikipedia below.

All my Algebraic life I've wondered what Wikipedia answers well:

"From the earliest use of mathematical notation multiplication took precedence over addition, whichever side of a number it appeared. Thus 3 + 4 × 5 = 4 × 5 + 3 = 23. When exponents were first introduced, in the 16th and 17th centuries, exponents took precedence over both addition and multiplication, and could be placed only as a superscript to the right of their base. Thus 3 + 5 2 = 28 and 3 × 5 2 = 75. To change the order of operations, originally a vinculum (an overline or underline) was used. Today we use parentheses. Thus, to force addition to precede multiplication, write (2 + 3) × 4 = 20."

Wikipedia points out that multiplication and division are of equal importance so that they can trade places. The same is true of addition and subtraction.

" These mnemonics may be misleading, especially if the user is not aware that multiplication and division are of equal precedence, as are addition and subtraction. Using any of the above rules in the order "addition first, subtraction afterward" would give the wrong answer to many equations."

10 - 3 + 2 figured left to right is 9

If you figured the addition first the answer is 5. The order of operations really matters.

Further…

The order of operations, or precedence, used in mathematics and many programming languages is expressed here:
terms inside parentheses or brackets
exponents and roots
multiplication and division As they appear left to right
addition and subtraction As they appear left to right

This means that if a mathematical expression is preceded by one operator and followed by another, the operator higher on the list should be applied first. The commutative and associative laws of addition and multiplication allow terms to be added in any order and factors to be multiplied in any order, but mixed operations must obey the standard order of operations.

It is helpful to treat division as multiplication by the reciprocal (multiplicative inverse) and subtraction as addition of the opposite (additive inverse). Thus 3/4 = 3 ÷ 4 = 3 • ¼; in other words the quotient of 3 and 4 equals the product of 3 and ¼. Also 3 − 4 = 3 + (−4); in other words the difference of 3 and 4 equals the sum of positive three and negative four. With this understanding, we can think of 1 - 2 + 3 as the sum of 1, negative 2, and 3, and add in any order: (1 - 2) + 3 = -1 + 3 = 2 and in reverse order (3 - 2) + 1 = 1 + 1 = 2. The important thing is to keep the negative sign with the 2.

The order of operations worksheets below reflect the left to right rule from Saxon's Math 7/6 page 495:

1. Simplify within Parentheses.
2. Simplify Exponential powers and roots.
3. Multiply and Divide from left to right.
4. Add and Subtract from left to right.

Thanks to Crewton Ramone and Teresa C for helping here!

Printable Order of Operations Worksheets

These thirteen order of operations worksheets are in order by difficulty. They offer room for copying and for figuring. 

They're a great visual way of learning the basic idea of the order in which we solve math problems.

Exponents Worksheets Build Easy Recognition

I made these printable Math exponent worksheets and charts to offer the practice necessary to become fast using exponents.

If your kids are not familiar enough with multiplication and division to tackle exponents, we have multiplication and division worksheets that are pure practice.

Negative exponents mean the reciprocal of the base raised to the power of the exponent.

Thank you for visiting our Order of Operations worksheets.

Check your answer with this Math problem solver .