Printable Prime Numbers Chart
Primes At-A-Glance

I like to keep a printable prime numbers chart handy for factoring. Below I have a list of prime numbers to print that you can keep in your or binder. 

Then have your students fill in our blank chart so that they can practice learning the main prime numbers and see the difference between prime and composite numbers. After that, I like the kids to keep a copy in their text book or notebook.

The first 100 prime numbers are more than enough for most elementary and high school applications. We also have prime number worksheets below.

Make A List Of Prime Numbers

Once your kids have seen how the first primes are found, the easiest way for them to tell whether a number is prime or not is to be able to reference a chart even if they only write the first 12 to 25 in their books.

I was so glad to read that Wikipedia says this, "There is no known useful formula that yields all of the prime numbers and no composites."

I had always wondered "How to figure primes" as a child, and I had also wondered again as our children began to learn.

I couldn't figure it myself, so, as they went through school, I began to have them keep a chart in the front of their books so that they could have their own list of prime numbers handy instead of us trying to figure each time. Each time they figured a new prime, they'd write it on their list.

Printable Prime Numbers Chart and Worksheets

You can print these prime number charts on card stock to keep for reference in your Math book or binder.

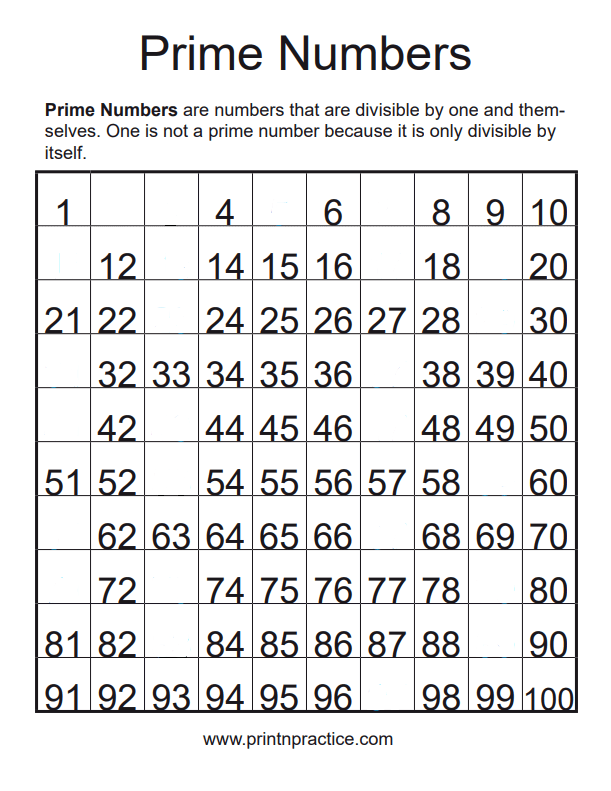
1. The first prime numbers chart has the 25 prime numbers that are in the first 100 numbers (in sequential order: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97). Except for the number 1, the composite numbers are black and the prime numbers are light blue. They can be traced for a quick memory exercise for small children. Use it as a poster or as a worksheet.
2. The second is a worksheet.
3. The next is a prime numbers worksheet with a small chart to cut and paste in a book or use as a bookmark. I like keeping ours in the front of our text books.
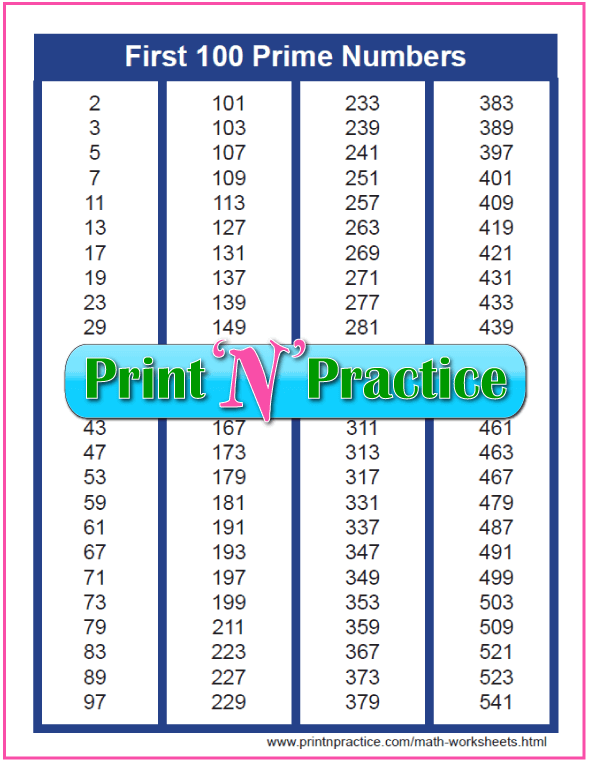
4. And the last is a printable list of the first 100 prime numbers to use in a binder or as a Math poster, etc. Most younger students do not need the first hundred prime numbers chart although it is a very handy item for teachers with bright students! :-)

Use this prime number chart as an answer key or a practice worksheet. Younger students can trace over the numbers. The next one has blank spaces.

See all our PrintNPractice printables in affordable bundles here .

Use A Prime Number List

The first primes are easy to memorize. If you'll teach your students to memorize the first of these, they'll have an easier time with factoring numbers.

Just practice a few times out loud and most students will be able to recognize the first primes in a week.

I also like to have them copy the list to the inside covers of their Math book or notebooks. This acts as a review and as a reference.

I would not ask them to memorize more than those in the first 100 numbers.

First 100 Prime Numbers

If you have high school math students, this chart is a handy one to keep in their binder. 

I do. :-)

Why not memorize more than the first 100 prime numbers?

Way back in Greece, about 300 years before Christ, Euclid said that there is an infinite number of prime numbers, so there is no sense in trying to learn a large number of them.

Today you can search for a prime number tool or a prime numbers chart online, or find a computer tool, which is so much easier. Keeping a chart handy, though, obviates the need to research or key up the computer.

I agree that, at first, it is good to have children figure whether a number is prime or not, but once that's figured and they understand; there's no need to re-figure the prime numbers for every single Math problem. It's much easier to keep a prime numbers chart, or a prime numbers list, handy. See my primes charts in PDF format above.

What Is A Prime Number?

Prime Number Definition: A prime number is a counting number that is greater than 1 and has only two factors; 1 and itself.

Which Are The Prime Numbers?

The first primes are 2, 3, 5, 7, and 11 because their only factors are 1 and themselves. You cannot divide them by any other number to get a whole number for an answer. There are 25 prime numbers on a 100s chart which is usually plenty for being able to discern which are prime and composite numbers. See our printable hundreds charts below.

I was taught, or perhaps I wrongly remember, that 1 was a prime number. I guess 1 is not a prime number. Here's what I've found.

0 is nullity. 1 is identity, it only has one factor. 2 is the only even prime number (think about it, all the other even numbers are also divisible by two making a third factor). Primes have only two factors, and composites have three or more factors. See them both on our prime numbers chart below.

Composite Numbers

A composite number is a counting number that is greater than one and has three or more factors, it has at least two prime numbers and 1 as factors. 4, 6, 8, and 10 are also divisible by 2 as well as 1 and themselves so they are composite numbers, meaning that they are composed of more numbers than one and themselves. 6, 9, and 12 are divisible by 3 so they are composite numbers, too.

Prime Factorization

Prime factorization is finding the prime factors in a composite number. The prime factors of 100 are 2 x 2 x 5 x 5.

With the right start, factorization can be like a game. It can be fun for some kids.

Teaching Prime Numbers

At first, it is really good to show your students how prime numbers are found. If you've got older students, go to Wikipedia to show them some of the formulas that have been developed over the years; but younger students simply need to see that primes only have 2 factors, 1 and the number.

It's very easy to take a hundreds chart (see above) and cross off the numbers that are multiples of other numbers. For instance and step-by-step:

1. Cross out 1 since it only has one factor, itself. (Make more impact by using different colors for each cross.)
2. Leave 2 since it only has two factors, then cross out all the numbers that are divisible by two which is every other column on the chart.
3. Leave 3 since it only has two factors, then cross out all the numbers that are divisible by three.
4. 4 is already marked.
5. Leave 5 since it only has two factors, and cross out all the numbers that are divisible by five, which really only means to cross out the fives column since the tens are crossed out by the twos.
6. 6 is already marked.
7. Leave 7 since it only has two factors, and cross out all the numbers that are divisible by seven.
8. All the rest of the numbers are prime numbers! Circle them and copy them to your notebook to make your own prime numbers chart. There are only 25 on a hundreds chart.

See

• Printable hundreds charts here.
• Printable Roman Numeral worksheets here.

Dan's got a wonderful website with a handy prime number checker. Go to Dan's prime number calculator here.

---

Check your answer with this Math problem solver .